Strumenti di misura della fluidodinamica
Le misure della velocità
dei fluidi sono divise in misure di valore locale e misure di valore medio
(detto anche portata).
Le apparecchiature e le
tecniche sperimentali d’impiego più frequente sono le seguenti:
a)
metodo della pesata
b)
tubo di Pitot
(-Prandtl)
c)
tubo di Venturi
d)
diaframma o
boccaglio
IL METODO
DELLA PESATA.
Tale metodo sfrutta
elementi d’uso comune: un pentolino, una bilancia, un cronometro e dei “buoni
riflessi”.
Il suo funzionamento è
abbastanza immediato:
a)
si mette il
pentolino sotto un getto d’acqua e “contemporaneamente” si fa partire il
cronometro
b)
quando il pentolino
è pieno si toglie dal getto e “contemporaneamente” si spegne il cronometro
(abbiamo il Dt)
c)
si pesa il pentolino
(troviamo la massa M)
d)
a questo punto
possiamo trovare la portata di massa nell’ unità di tempo
![]() ( 1 )
( 1 )
La precisione di questa tecnica di misurazione è ovviamente legata all’ accuratezza con cui si provvede alla raccolta della massa M e alla precisione degli strumenti di misura (bilancia e cronometro); in genere l’ errore complessivo è inferiore all’ 1%.
TUBO DI
PITOT (-PRANDTL)
E’ un misuratore di velocità locale; in questa versione (con la variante di
Prandtl) è molto usato per la misura in
aria ed è indifferente che l’ aria sia in movimento rispetto allo strumento o
viceversa (per esempio è usato in aeronautica per misurare la velocità relativa
dell’ aeromobile rispetto all’ aria esterna).
Il tubo di Pitot può essere di diverse misure, generalmente si va da
lunghezze di un metro e diametro di qualche centimetro, a lunghezze di qualche
centimetro con diametro di qualche millimetro; il tubo è principalmente prodotto
in acciaio per prolungarne la durata, è costituito da due tubi concentrici e
coassiali sagomati a “ L “ (ruotata di 180°) e nella parte più corta (testa),
pari ad una ventina di diametri, sono presenti i fori per il rilevamento della
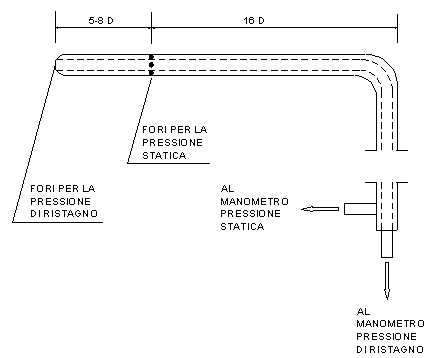
pressione di ristagno e della pressione statica (fig. 1).
FIGURA 1: tubo di Pitot, vista laterale
FIGURA 2: tubo di Pitot, sezione laterale, dettaglio
della testa
Lo strumento va puntato con la testa nella direzione in cui scorre il fluido
di cui si vuole misurare la velocità.
Come si nota in figura 1, il tubo è chiuso all'estremità opposta alla
testa, all'inizio del gambo, in quanto vi è il manometro; il fluido entra
all'inizio nel tubo, ma una volta riempiti gambo e testa, vede il tubo come
chiuso frontalmente.
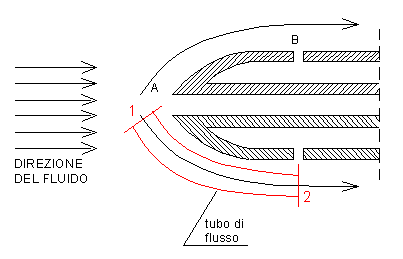
E' costretto quindi a girare
intorno alla punta della testa, come indicato in figura 2.
All'imboccatura della testa si ha evidentemente velocità nulla, e di
conseguenza un massimo di pressione; ad una distanza dalla punta di circa 5-8
diametri, in corrispondenza dei fori laterali, il fluido ha riacquistato la
velocità che aveva all'infinito, prima di arrivare alla testa, e in questo
punto viene presa la pressione statica.
Ora, se si prende un tubo di flusso del tipo mostrato in figura 2, come
sezione 1 quella al punto di ristagno e come sezione 2 quella davanti ai fori,
si può scrivere l'equazione di Bernoulli; il tubo è infinitesimo, quindi non si
usa la velocità media, ma la velocità locale.
![]() (
1 )
(
1 )
L'equazione viene posta uguale a zero in quanto lungo il tubo di flusso
considerato non sono presenti pompe o ventole di alcun genere.
Sono possibili alcune semplificazioni, in particolare:
·
si possono
trascurare le perdite di carico R,
in virtù del fatto che il percorso è molto corto, e che lo strumento è
progettato per favorire uno scorrimento aerodinamico del fluido;
·
si può trascurare la
variazione di quota z2-z1;
per la disposizione geometrica dei fori, posti intorno alla testa, il
baricentro del tubo di flusso è alla stessa quota;
·
la velocità u1 è nulla in quanto 1 è un punto di ristagno.
Semplificando otteniamo quindi:
![]() (
2 )
(
2 )
da
cui si ricava immediatamente l'espressione della velocità u2:
![]() (
3 )
(
3 )
Non è possibile misurare
velocità che variano molto con il solo ausilio del manometro a causa degli
elevati salti di pressione, per questo si ricorre all’ ausilio di un
micromanometro a tubo inclinato di tipo idraulico (fig. 3) o ad un
micromanometro differenziale ad “U”
(fig. 4).
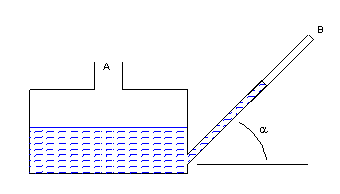
FIGURA 3: micromanometro a tubo inclinato
IMMAGINE IN COSTRUZIONE!!!
Il micromanometro a tubo inclinato è
costituito da un serbatoio con un vasto pelo libero, comunicante con un
tubo capillare di vetro inclinato.
Il serbatoio ed il tubo comunicano (attraverso A e B) con gli ambienti nei
quali sussistono le pressioni p1
e p2.
Sul tubo è disposta una scala di lettura; dall’entità dello spostamento verticale del liquido nel tubo si risale alla differenza di pressione p2-p1.
Lo strumento aumenta la sua sensibilità al diminuiradell’angolo a.
Nel micromanometro differenziale a “U” utilizzo il dislivello di un liquido
per misurarne la pressione
TUBO DI
VENTURI
E’ un misuratore di
velocità media di un fluido che scorre in un condotto; dà luogo ad una
differenza di pressione.
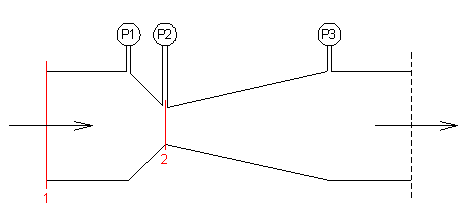
FIGURA 5: tubo di Venturi, sezione laterale
Come si può osservare in figura 5, lo strumento è costituito da un tubo con
una brusca riduzione di sezione nella zona tra 1 e 2, e da un ritorno molto più
graduale alla sezione iniziale, tra 2 e 3.
Il manometro 3 non è di utilità diretta nella misura della velocità, in
quanto serve per controllare che la pressione sia ritornata la stessa che si ha
in 1; questo è necessario in quanto il tubo di Venturi è uno strumento che non
deve dar luogo a perdite di carico lungo il circuito idraulico.
In questo caso viene calcolata la velocità media, mettendola in relazione
con la pressione, tramite l'equazione di continuità; tale equazione viene
scritta per il tubo di flusso che ha come sezione iniziale e finale le sezioni
1 e 2, e come profilo laterale lo stesso tubo.
Dall'equazione di Bernoulli, supposto il condotto orizzontale ed il fluido
incomprimibile, si ha:
![]() (
4 )
(
4 )
Il problema, rispetto al tubo di Pitot, è che in questo caso compaiono due
velocità; si tratta quindi di esprimere una velocità in funzione dell'altra,
tramite una relazione ottenuta dall'equazione di conservazione della massa.
![]() (
5 )
(
5 )
da
cui:
![]() (
6 )
(
6 )
dove
S1 e S2 sono le aree delle superfici delle sezioni di entrata
e di uscita.
Se la densità r viene supposta costante (fluido incomprimibile),
è possibile semplificarla.
Trattandosi di sezioni circolari, la superficie è proporzionale al quadrato
dei raggi, quindi:
![]()
![]()
(
7 )
da
cui si ricava la velocità w2
in funzione di w1:
![]() (
8 )
(
8 )
Si sostituisce ora l'espressione della velocità w2 nell'equazione
( 4 ):
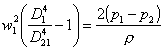 (
9 )
(
9 )
In questo modo si ottiene l'espressione della velocità w1:
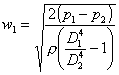 (
10 )
(
10 )
DIAFRAMMA
O BOCCAGLIO
Sono due misuratori di portata molto simili, basati sull'intruduzione
volontaria in un condotto di una perdita di carico concentrata.
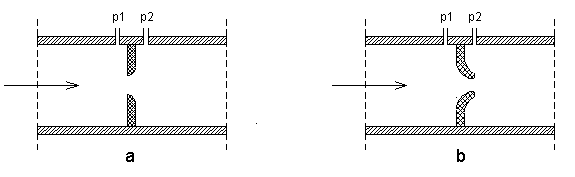
FIGURA 6: diaframma (a) e boccaglio (b), sezioni laterali
Se l'accidentalità che deve dar luogo alla perdita di carico è un disco
forato, lo strumento viene detto diaframma;
se invece si utilizza un convergente a forma di campana, viene detto boccaglio.
Tramite i piccoli tubi che stanno a monte e a valle dell'ostacolo si rileva
una differenza di pressione Dp, matematicamente:
![]() ( 1 )
( 1 )
Se il diametro è lo stesso prima e dopo l’ ostacolo, la densità non cambia pertanto non cambia nemmeno la velocità (quella di entrata è uguale a quella di uscita) in definitiva possiamo elidere il primo termine della equazione; allo stesso modo, essendo il tubo posto in posizione orizzontale, non si presenta un variazione di altezze pertanto possiamo elidere anche il secondo termine in definitiva:
![]() ( 2 )
( 2 )
dove
![]() (
3 )
(
3 )
pertanto:
![]() (
4)
(
4)
da cui si ricava la velocità w:
![]() (
5 )
(
5 )
Il funzionamento, visto da fuori, e' identico a quello del tubo di Venturi;
la differenza è che il tubo di Venturi introduce una perdita di carico
trascurabile, mentre il boccaglio introduce una forte perdita di carico.
Può essere messo permanentemente nel circuito idraulico: in questo caso non
altera la misura, in quanto, essendo parte del circuito, la sua perdita viene
calcolata insieme alle altre perdite nel progetto della pompa.