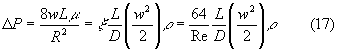
Fluidodinamica
Argomenti della lezione :
Definizioni di carattere generale
Viscosità
Legge di Newton
Esperimento di Reynolds
Numero di Reynolds
Problema di Poiseuille
La fluidodinamica è la branca della fisica meccanica che studia il moto dei fluidi in tutte le sue varie forme . Tali moti si dividono in interni , vale a dire dentro i condotti , ed esterni . Di questi ultimi sono di particolare interesse le applicazioni aerodinamiche in genere .
Il punto da cui partire per iniziare uno studio di fluidodinamica è la forza d’attrito . Alla base dei ragionamenti che si faranno in questa lezione c’è una legge detta di Newton ed una grandezza chiamata viscosità .
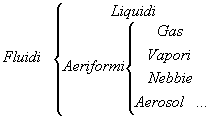
Fluido = sostanza che non ha forma e volume proprio ; si adatta infatti al recipiente che lo contiene .

La caratteristica fondamentale dei liquidi è il possedere un proprio volume e di essere perciò incomprimibili ( v = cost e di conseguenza r = cost ) , mentre quella degli aeriformi è la comprimibilità . Entrambi sono accomunati dal non avere una forma , ma dal seguire l’andamento del recipiente che li contiene . La branca della fluidodinamica che studia i liquidi si chiama Idraulica . Le stesse considerazioni che verranno fatte per i liquidi hanno validità anche per gli aeriformi , solo se è lecita
l‘ipotesi di r = cost .
Viscosità
= grandezza fisica , propria dei fluidi , che indica come essi trasmettano sforzi tangenziali .
Il sistema è formato da una lastra piana immersa in un fluido in moto . Si definisce :
Bordo d’attacco = il punto in cui il fluido investe il corpo
Strato limite dinamico = luogo dei punti la cui velocità del fluido raggiunge il 99% di quella del sistema prima del incontro con il corpo ( valore che chiameremo u¥ ) . Lo spessore di tale strato si indica con d . Questo spessore varia con la distanza x dal bordo d’attacco ed è simmetrico rispetto alla parete . Dalla definizione di strato limite dinamico si ha che
![]()
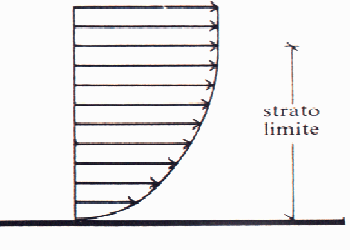
Fig. 1 - Variazione della velocità fino allo strato limite

Fig. 2 - Lo strato limite
Tale strato divide il fluido in due zone di influenza :
Suddividiamo ora gli sforzi in due categorie :
entrambi riferiti alla parete che interagisce con il fluido .
Mentre i primi sono dovuti alla pressione prodotta dalle particelle del fluido , che si può raffigurare microscopicamente come un insieme di palline che muovendosi caoticamente colpiscono la parete in esame , i secondi sono legati al concetto di viscosità , in quanto sono generati da essa.
A livello ideale , un fluido privo di effetti viscosi interagisce con soli sforzi normali . Analogamente i solidi , in mancanza di attrito , scivolano gli uni su gli altri senza la necessità di vincere forze opposte al moto .
Come l’attrito anche la viscosità comporta la degradazione di energia meccanica in energia termica .
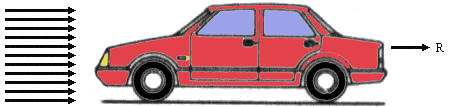
Fig. 3 - Sulle pareti inclinate , il fluido crea sforzi normali e tangenziali insieme ,
producendo una risultante di direzione comune R .
Legge di Newton
Ipotesi :
L’ipotesi di aderenza sta nel fatto che per quanto un fluido lambisca rapidamente la parete di un corpo , tale che la velocità relativa parete-fluido sia diversa da zero , esso diminuirà tale velocità con l‘avvicinarsi al corpo . Lo strato di fluido distante un infinitesimo dalla parete è aderente alla stessa e perciò la sua velocità è nulla .
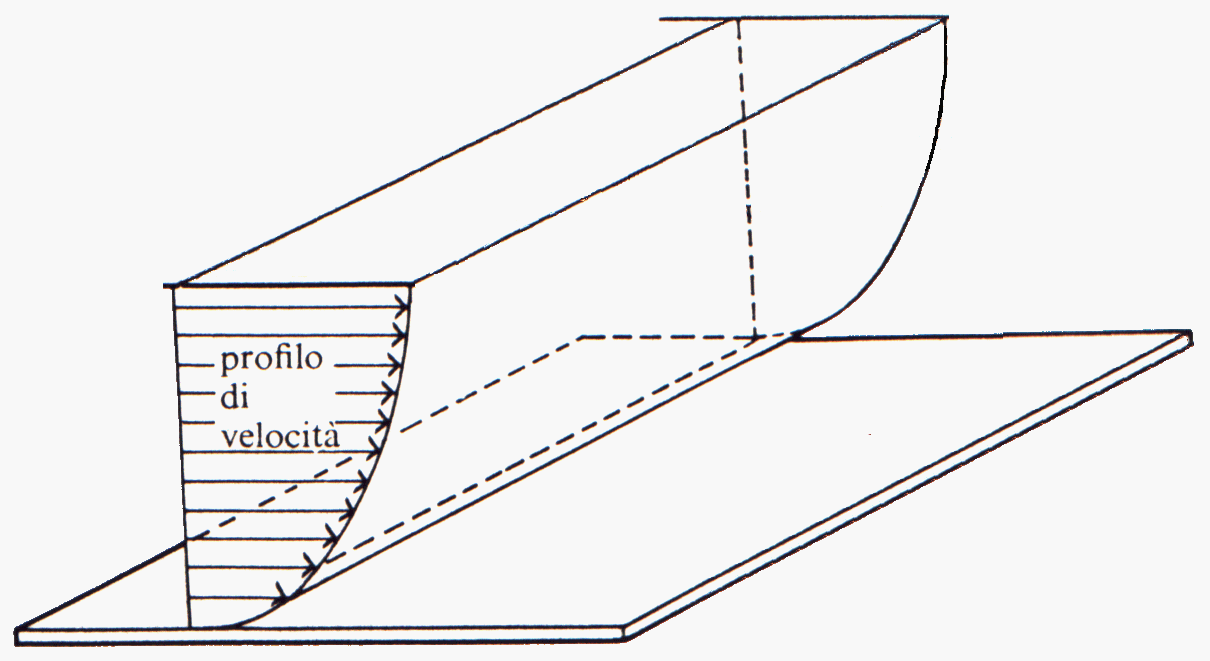
Fig. 4 - Profilo delle velocità al variare della distanza dalla parete
La legge di Newton ci dice che se abbiamo un fluido in moto , che interferisce con un corpo solido , in prossimità dello stesso il fluido è sempre fermo . Lo sforzo tangenziale è proporzionale alla viscosità per la velocita di scorrimento ![]() (che si misura in
(che si misura in ![]() ) . Per piccoli valori di questa velocità tutti i fluidi seguono la legge di Newton .
) . Per piccoli valori di questa velocità tutti i fluidi seguono la legge di Newton .
![]()
t sforzo tangenziale , si misura in Pa
u velocità
n normale alla parete
p parete
Su un diagramma relativo ad un fluido Newtoniano , che riporta t ( in Pa ) in funzione della velocità di scorrimento , si rappresenta la viscosità con la pendenza della retta .
I fluidi si dividono in :
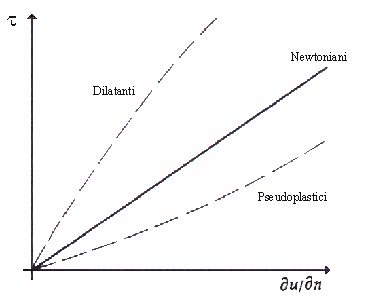
Fig. 5 - Diagramma dei fluidi viscosi
I fluidi non Newtoniani hanno
memoria . Se si sta mescolando uno di questi e si decide di diminuire la velocità dell’operazione , non si percorre sul grafico il cammino appena seguito in direzione opposta , ma si compie un ciclo chiamato isteresi dei fluidi non Newtoniani . Le isteresi sono diverse a seconda che il fluido sia pseudoplastico o dilatante .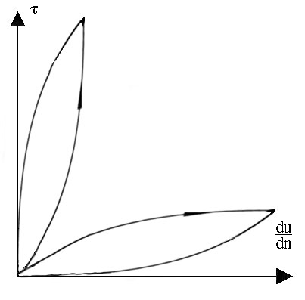
Fig. 6 - Diagramma d’isteresi
Come si misura la viscosità ?
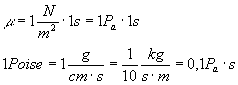
Oltre alla normale viscosità con connotazione dinamica ne esiste una di tipo cinematico , che s’indica con n e da com’è definito rappresenta un rapporto tra le forze viscose e quelle d’inerzia
![]()
e si misura in ![]() .
.
Ad esempio per l’acqua dove r
=1000 ![]() , la viscosità è 1000 volte più piccola di quella cinematica . Le due grandezze esprimono lo stesso concetto fisico degli sforzi tangenziali , ma è come se n
fosse "normalizzata" attraverso l’inerzia del fluido . Le particelle tendono ad allontanarsi tanto più velocemente quanto più sono pesanti , ossia a parità di sforzo viene frenata più facilmente una corrente fluida a bassa densità , che non una ad alta densità . Un elevato valore di n
è indice di un fluido molto leggero ma più portato a frenare per attrito , viceversa un basso valore indica che il fluido si oppone in modo minore al moto reciproco fluido parete .
, la viscosità è 1000 volte più piccola di quella cinematica . Le due grandezze esprimono lo stesso concetto fisico degli sforzi tangenziali , ma è come se n
fosse "normalizzata" attraverso l’inerzia del fluido . Le particelle tendono ad allontanarsi tanto più velocemente quanto più sono pesanti , ossia a parità di sforzo viene frenata più facilmente una corrente fluida a bassa densità , che non una ad alta densità . Un elevato valore di n
è indice di un fluido molto leggero ma più portato a frenare per attrito , viceversa un basso valore indica che il fluido si oppone in modo minore al moto reciproco fluido parete .
Esperimento di Reynolds
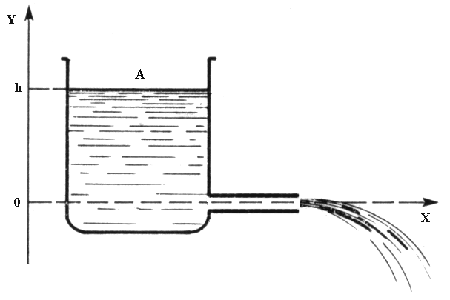
Fig. 7 - Attrezzatura utilizzata da Reynolds .
Figura di spicco della fluidodinamica moderna è Reynolds , studioso dei moti dei fluidi entro i condotti di sezione circolare .
Preso un serbatoio pieno d’acqua e praticata un’apertura sulla parete , alla quale è collegato un tubo di materiale trasparente , originariamente vetro , è possibile studiare l’andamento del liquido nel condotto al variare della sua velocità w .
![]()
![]()
Per la (4) , si crea una variazione di portata nel tubo ( da cui deriva la variazione di velocità w ) solo variando la distanza dal pelo libero dell’acqua h .
Numero di Reynolds
Il risultato ottenuto inserendo nel condotto un liquido rivelatore colorato è il seguente :
![]()
![]()
![]()
Una volta scoperto sperimentalmente che la transizione da un regime all altro era caratterizzata dal valore costante del prodotto velocità per il diametro del condotto , il passo successivo era la definizione di un parametro di controllo chiamato numero di Reynolds . La transizione laminare turbolento avveniva in funzione della viscosità cinematica a valore di Re » 3000 , anche se più realisticamente si suole parlare di moto laminare per valori sotto il 2300 e di moto turbolento al di sopra del 4100 . All interno di tale intervallo non è possibile fare una previsione sul comportamento del sistema .
Il numero di Reynolds è un numero puro e perciò non dipende dal sistema di misura delle grandezze utilizzato .

Fig. 8 - Differenze tra moto laminare e moto turbolento
L’importanza di tale fenomeno è evidente nel caso del condotto di raffreddamento . Fornendo una quantità di calore Q , il liquido in regime laminare si scalda e la sua temperatura cala in modo graduale con la distanza dalle pareti del tubo . Forzando una situazione turbolenta invece si riesce a fare assorbire al liquido quantità di calore maggiori , migliorando le prestazioni del sistema .
Questo è il caso tipico dell impianto di raffreddamento di un’automobile , che viene dimensionato per un liquido con determinati valori di viscosità e di densità , per avere al suo interno un regime turbolento . Il funzionamento con un fluido non adeguato porta al surriscaldamento , al funzionamento anomalo ed infine al danneggiamento delle componenti meccaniche .
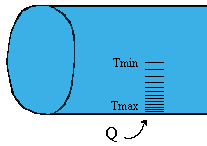
Fig. 9 - Sviluppo termico del fluido con la distanza dal tubo .
Problema di Poiseuille
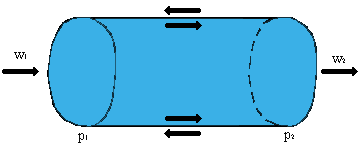
Fig. 10 - Sistema studiato da Poiseuille
Ipotesi :
Si vuole determinare la perdita di pressione ( o come viene chiamata in gergo di carico ) del fluido attraverso il tubo dovuta a fenomeni di tipo viscoso . Il fenomeno della riduzione di pressione è connesso agli sforzi tangenziali che il fluido scarica sulle pareti del condotto , cosicchè il fluido muovendosi spinge il condotto nella direzione del moto . Dalle ipotesi precedenti si ricava che
![]()
Dall’equilibrio delle forze che agiscono sul fluido :
![]()
![]()
Dall’ipotesi di regime sviluppato abbiamo che ![]() e da quella dell’aderenza sappiamo che
e da quella dell’aderenza sappiamo che ![]() , da cui
, da cui
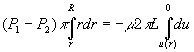
da cui
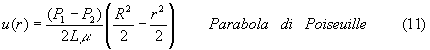
Questa parabola indica il profilo della velocità del liquido nel tubo . Noto infine che u è sempre parallelo alla normale alla superficie A , si trova la velocità media w :
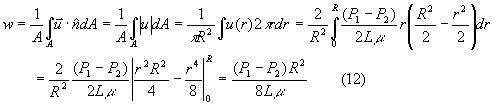
Sostituendo la (12) nella (11) si ottiene :
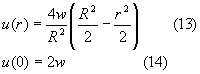
ossia il valore massimo della velocità u , che vale esattamente il doppio di quanto non si avrebbe se il profilo fosse piatto . Tale valore coincide con il vertice della parabola di Poiseuille .
Considerando un nuovo parametro adimensionale x chiamato fattore d’attrito , legato al numero di Reynolds dalla relazione
![]()
![]()
si trova l’espressione cercata per la perdita di carico :