Umberto
Guareschi – 127190 - Lezione del 20-12-2001. ore 16:00-18:00.
Calcolo
delle Perdite di Carico.
INTRODUZIONE.
Per introdurre l’argomento mi sembra importante partire da una definizione fondamentale:definiamo FLUIDO una sostanza che non è in grado di resistere alle deformazioni, o più precisamente, che presenta una resistenza bassa o addirittura nulla alle forze di taglio. Nella nostra trattazione, l’esatta struttura molecolare di un fluido non gioca un ruolo diretto nella sua descrizione. Possiamo quindi trattare i fluidi come mezzi continui. Una data massa di fluido ha un volume definito. Poiché il fluido è completamente deformabile, esso assume la forma del recipiente che lo contiene.
RAPPRESENTAZIONE E CLASSIFICAZIONE DEI FLUIDI IN MOVIMENTO.
Poiché stiamo studiando la Fluidodinamica, consideriamo i
fluidi in movimento. Se rappresentiamo la direzione della velocità in un dato
punto con un vettore applicato nel punto, con la lunghezza proporzionale al
modulo della velocità, otteniamo una rappresentazione come in Fig.

Per flusso stazionario (indipendente dal tempo), si parla di velocità locale v( r ). Se consideriamo un punto fissato, l’elementino di fluido che si trova in quel punto si muove nella direzione del vettore velocità. Un istante più tardi, l’elementino si trova in un punto adiacente, con vettore velocità leggermente diverso. Questo vettore definisce la direzione dell’elementino di fluido e la velocità di moto nell’istante successivo. Ancora un istante dopo, la velocità locale, che sarà variata solo di poco, determina il tratto successivo del moto. In questo modo, si può tracciare la traiettoria di un elementino di fluido. La traiettoria di un piccolo elemento di fluido che mantiene la propria integrità è chiamata linea di corrente. Le linee di corrente si possono visualizzare introducendo una sostanza campione (colorata) nel fluido in movimento. Quando il flusso è stazionario, questa segue una linea di corrente.
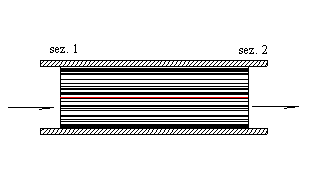
Le linee di corrente non possono mai intersecarsi, eccetto che nei punti in cui si annulla la velocità, poiché un vettore velocità non può avere contemporaneamente due direzioni. Il flusso descritto da linee di corrente è chiamato flusso laminare; nel flusso laminare, ciascun elemento di fluido viaggia lungo una traiettoria regolare e ben definita. Sotto certe condizioni il flusso cessa di essere laminare e diventa turbolento. In presenza di flusso turbolento, come quello di un corso d’acqua, velocità e pressioni risultano rapidamente variabili.
In linea di principio, il moto di un fluido si può descrivere pensando di dividere il fluido in piccoli elementi ed applicando a ciascuno di questi la seconda legge di Newton; ma quando abbiamo a che fare con forze conservative e non siamo interessati ad un’informazione di carattere vettoriale, la conservazione dell’energia è una valida alternativa alla seconda legge di Newton.
Se il fluido non è viscoso, cosicché non vi è dissipazione di energia, e il fluido è incomprimibile, in modo da assicurare che la densità rimanga costante, la conservazione dell’energia per i fluidi diventa di formulazione immediata. Questa ci fornirà una relazione semplice e potente attraverso la quale descrivere il moto.
EQUAZIONE DI BERNOULLI:
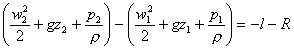
Con ![]() = velocità,
= velocità, ![]() = cost. gravitazionale,
= cost. gravitazionale,
![]() = pressione,
= pressione, ![]() = densità,
= densità, ![]() = lavoro,
= lavoro, ![]() = resistenza, z =
quote piezometriche.
= resistenza, z =
quote piezometriche.
DEFINIZIONE E CLASSIFICAZIONE DELLE PERDITE DI CARICO.
Bernoulli dimostra dunque come si possa parlare si
conservazione di energia anche in un sistema formato dal moto di un fluido
all’interno di un condotto, senza però trascurare il contributo totale degli
scambi di energia con l’esterno e il valore della resistenza.
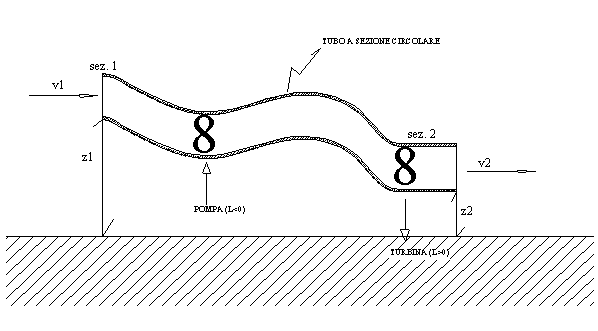
Parliamo per entrambi di perdite di carico.
Quelli che abbiamo definito con il termine scambi di energia con l’esterno, non sono altro che gli effetti di turbine o di pompe, tramite le quali siamo in grado rispettivamente di produrre energia sfruttando il movimento del fluido (definiamo quindi Lavoro > 0), oppure di dare energia al fluido ( L < 0 ).
Il calcolo della resistenza (dissipazione di energia convertita in calore) è invece di trattazione un po’ più complessa.
Innanzitutto distinguiamo (attraverso una classificazione puramente utilitaristica) le perdite di carico in concentrate e distribuite.
Possiamo affermare che:
![]()
In un tubo a sezione continua, libero, dritto, perfettamente uniforme si manifesta una perdita di calore pari a
![]() ,
, 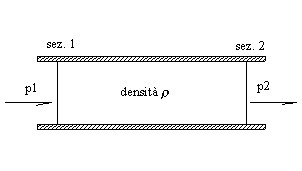
la resistenza varierà cioè in funzione della lunghezza tra la sezione 1 e la sezione 2. (caso di perdite distribuite).
Le perdite concentrate sono invece quelle dovute ad accidentalità introdotte all’interno del tubo (ad es. un rubinetto).
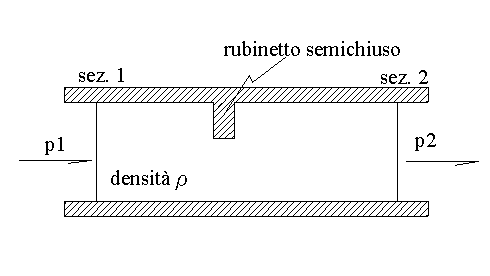
CALCOLO DELLE PERDITE DI CARICO.
Per stabilire la causa e determinare l’intensità delle perdite di carico, gli studiosi si sono affidati ad un potente strumento, spesso utilizzato per risolvere questioni altrimenti irrisolvibili, il principio di similitudine, il quale afferma che a problemi geometrici simili si ottengono medesime soluzioni.
Caso 1: P.
di C. distribuite.
In seguito ad esperimenti, è stato
notato che R dipende dalla scabrezza ( ![]() ), dal diametro del tubo (
), dal diametro del tubo (![]() ) e dal numero di Reynolds ( Re):
) e dal numero di Reynolds ( Re):
![]() .
.
E’ immediato pensare al contributo del diametro del tubo e del numero di Reynolds (che mi definisce il manifestarsi o meno di condizioni di turbolenza), ma forse è meglio soffermarsi un attimo sulla scabrosità. Quest’ultima è sempre presente nei problemi pratici; non è infatti lecito pensare che possa esistere un tubo completamente liscio. Per quanto possa essere regolare, la superficie interna (quella a contatto con il fluido in movimento) presenterà sempre una certa irregolarità ( per quanto essa possa essere contenuta nell’ordine del mm, del decimo di millimetro, ecc...).
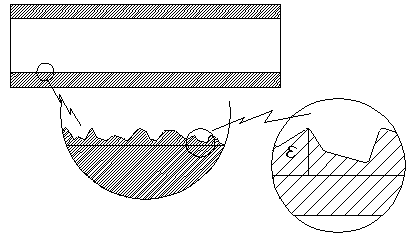
E’ sufficiente conoscere queste tre grandezze per conoscere il valore di R.
Empiricamente si è ottenuta la seguente:
![]() . In
cui abbiamo definito con
. In
cui abbiamo definito con ![]() il coefficiente d’attrito.
il coefficiente d’attrito.
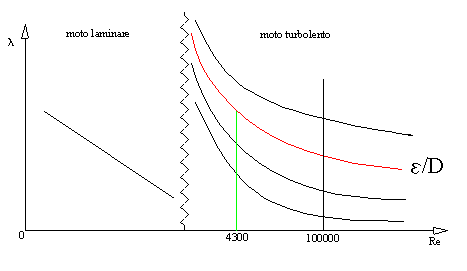
ABACO ( O DIAGRAMMA ) DI MOODY.
Grazie alla precedente equazione è stato possibile disegnare il seguente grafico, in cui si distinguono il moto laminare e il moto turbolento, separati da un certo valore Re di confine. Nella zona di transizione (peraltro molto ristretta), il comportamento del fluido è ambiguo; generalmente si cerca di dare una descrizione sommaria del moto prendendo valori intermedi ai due casi.
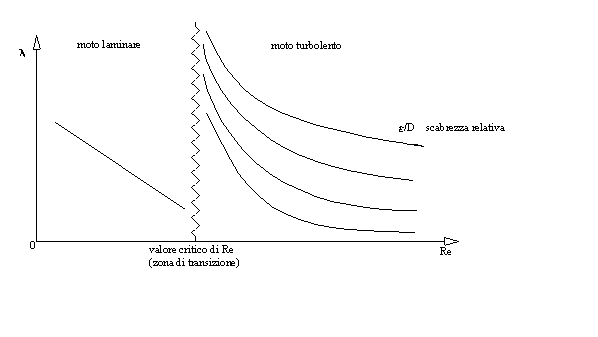
· Nel
moto laminare le perdite sono inferiori, ogni filetto ha una storia a se (non
si influenzano a vicenda in quanto sono tutti paralleli). Da notare come ![]() sia una che vale sempre
(nel caso laminare):
sia una che vale sempre
(nel caso laminare):
![]() .
.
· Il moto turbolento è più comune perché sono più comuni i tubi scabri ( già visto ); anzi, spesso si preferisce trovarsi in questo caso, in quanto la turbolenza favorisce il rimescolamento e questo favorisce lo scambio di calore ( es. negli impianti di riscaldamento).
Grazie al diagramma di Moody è
possibile ricavarsi ![]() ( e quindi il valore
della perdita ) in modo diretto, semplicemente conoscendo
( e quindi il valore
della perdita ) in modo diretto, semplicemente conoscendo ![]() e Re.
e Re.
Se mi trovo in situazione di moto molto
turbolento ( Re molto alto ) è interessante vedere che la curva tenda a
diventare una linea orizzontale ![]() è quindi possibile
ricavare direttamente il valore di
è quindi possibile
ricavare direttamente il valore di ![]() da
da ![]() per ogni valore di Re
sufficientemente grande.
per ogni valore di Re
sufficientemente grande.
DIAMETRO EQUIVALENTE.
Fino ad ora abbiamo parlato di diametro in quanto abbiamo sempre considerato tubi cilindrici ( e quindi a sezione circolare ).
![]() Il discorso e
le formule sono comunque estendibili a qualunque caso generico introducendo il
concetto di diametro equivalente ( De ).
Il discorso e
le formule sono comunque estendibili a qualunque caso generico introducendo il
concetto di diametro equivalente ( De ).
In generale ![]() , con A = Area di sezione e
, con A = Area di sezione e
![]() = Il Perimetro del
condotto bagnato dal fluido.
= Il Perimetro del
condotto bagnato dal fluido.
Es.
 per un quadrato di lato L
per un quadrato di lato L
![]()
![]() ;
;
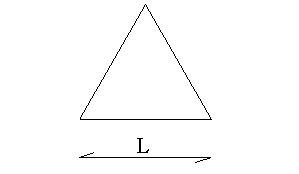 per un triangolo equilatero di lato L
per un triangolo equilatero di lato L 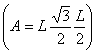
![]()
![]() .
.
Nel caso di sezioni in cui ci sia un moto a canaletta ( es. lo scolo di un canale )
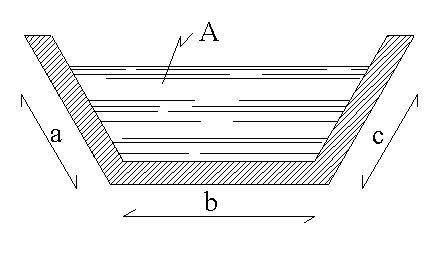
![]() .
.
Caso 2 : P.di C. concentrate.
Per quanto riguarda il caso di perdite di carico concentrate, è stato possibile ricavare in laboratorio i valori più significativi e riportarli in una tabella.
In generale: ![]() , con
, con ![]() = coefficiente in
funzione della geometria.
= coefficiente in
funzione della geometria.
Es.
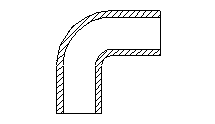 Gomito a 90°
Gomito a 90° ![]()
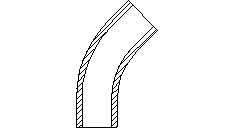 Gomito a 45°
Gomito a 45° ![]()
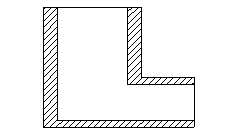 Imbocco (es. collegamento tra un serbatoio e un tubo)
Imbocco (es. collegamento tra un serbatoio e un tubo) ![]()
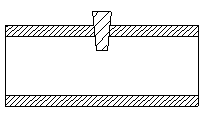 Valvola a
serracinesca aperta ( c’è sempre un po’ di perdita )
Valvola a
serracinesca aperta ( c’è sempre un po’ di perdita ) ![]()
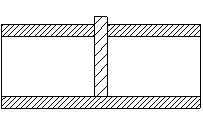 A rubinetto
completamente chiuso
A rubinetto
completamente chiuso ![]() ¥.
¥.
CONCETTO DI LNGHEZZA EQUIVALENTE.
E’ possibile ricondurre la discontinuità ad una lunghezza, ricollegandosi al concetto di perdita distribuita.
![]() .
.
DIAGRAMMA SPERIMENTALE.
In alternativa alla formula è stato anche ricavato, in seguito ai risultati di laboratorio, il seguente diagramma:
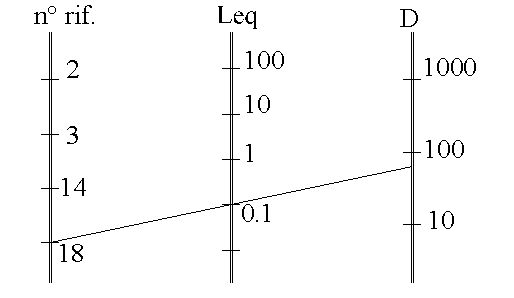
Ad ogni numero è stato abbinato un caso di studio ( es. gomito a 90°, valvola aperta, …)
Dato il numero corrispondente e D,
l’intersezione tra i due valori mi determina la ![]() ( ma forse è più
comodo utilizzare la formula).
( ma forse è più
comodo utilizzare la formula).
ESERCIZI SVOLTI.
1. Calcolare la velocità di uscita e la portata di un tubo alimentato da un serbatoio conoscendo i seg. Valori:
H = 2 m 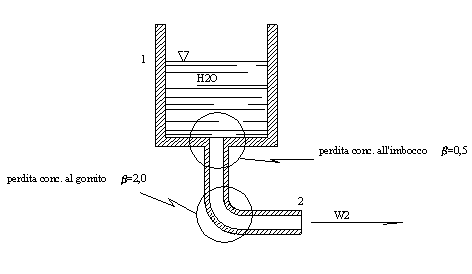
D = 2
L = 4 m
e = 20 mm
![]() Applico il teorema di Bernoulli.
Applico il teorema di Bernoulli.
![]() Notiamo che
Notiamo che ![]() e che
e che 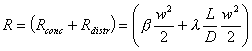 con
con ![]() .
.
L’incognita è ![]() . Risolvendo
l’equazione troviamo che
. Risolvendo
l’equazione troviamo che 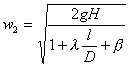 .
.
Questa è una formula molto comoda perché permettere di risolvere questo caso molto comune!
Non conosco l, ma conoscendo e posso procedere per iterazione, e ricavarmela utilizzando il diagramma di Moody ed una tabella, nella quale registrerò i vari tentativi grazie ai quali, con un po’ di pazienza, mi porteranno a conoscere un valore ben approssimato di w.
Procedere per
tentativi significa assegnare inizialmente un valore di l a piacimento ( per comodità
conviene sempre partire dal caso di perfetta turbolenza, per avere una
corrispondenza diretta tra ![]() e l) e ricavare di conseguenza la
e l) e ricavare di conseguenza la ![]() corrispondente.
Procedo in questo modo fino a quando
corrispondente.
Procedo in questo modo fino a quando ![]() .
.
|
N° tentativo |
|
Re |
l |
|
|
1 |
|
|
0.023 |
2.20 m/s |
|
2 |
2.20 |
44000 |
0.0247 |
2.156 m/s |
|
3 |
2.156 |
43000 |
0.025 |
2.15 m/s |
Al 3° tentativo posso considerare la mia approssimazione più che valida. Þ Ho trovato la velocità dell’acqua.
W = 0,15 m/s
![]() .
.
Questo non è un procedimento molto semplice, all’inizio. Ma basta un po’ di pratica per abituarsi e renderlo quasi immediato.
NOTA : Solitamente i problemi che ci vengono richiesti propongono situazioni estreme ( o tutti a dx o tutti a sx nel diagramma).
Nel
caso mi trovassi nel caso di moto laminare non conviene procedere per
tentativi! Esiste già la comoda
relazione ![]() .
.